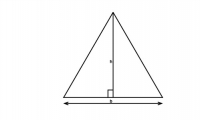
Comment calculer l'aire d'un triangle

Taille de police Réduire la taille de la police Augmenter la taille de police

L'aire d'un triangle est l'aire de la portion du plan qu'il enferme. Il existe plusieurs manières de la calculer, selon les informations dont on veut partir.

Cas particulier du triangle rectangle

Dans le cas d'un triangle rectangle et lorsuqe l'on connaît la largeur (l) et la longueur (L) de celui-ci il suffit de faire :

Aire = (L*l)/2

Calcul à partir d'une hauteur

Si le triangle est rectangle il est immédiat que son aire est

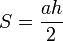
$S = \dfrac{ah}{2}$

où a est la longueur d'un côté différent de l'hypoténuse et h la longueur de la hauteur issue de ce côté. Si le triangle n'est pas rectangle, la relation reste vraie, car le triangle se décompose en deux triangles rectangles (comme sur la figure ci-dessous).

À partir des longueurs des trois côtés

Pour une expression de l'aire d'un triangle dont les longueurs des côtés sont a, b et c et p le demi-périmètre

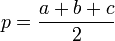[ $p=\dfrac{a+b+c}{2}$ ]

, on peut utiliser la formule de Héron :

$Aire = \dfrac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}=\sqrt{p(p-a)(p-b)(p-c)}$

À partir des coordonnées des sommets

L'aire du parallélogramme défini par deux vecteurs $\overrightarrow{u}$ , $\overrightarrow{v}$ est la norme de leur produit vectoriel :

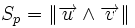
$S_p = \left\|{ \overrightarrow{u} \wedge \overrightarrow{v}}\right\|$

On peut calculer l'aire d'un triangle à partir de cette formule :

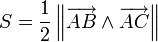$S = \dfrac12 \left\|{ \overrightarrow{AB} \wedge \overrightarrow{AC}}\right\|$ .

Un repère orthonormé étant donné, l'aire du triangle ABC peut être calculée à partir des coordonnées des sommets.

Dans le plan, si les coordonnées de A, B et C sont données par $A (x A, y A)$ , $B (x B, y B)$ et $C (x C, y C)$ , alors l'aire S est la moitié de la valeur absolue du déterminant

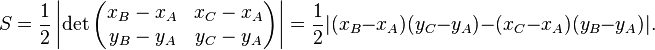
$S=\dfrac{1}{2}\left|\det\begin{pmatrix}x_B-x_A & x_C-x_A \\ y_B-y_A & y_C-y_A \end{pmatrix}\right| = \dfrac{1}{2}|(x_B-x_A)( y_C-y_A) - (x_C-x_A) (y_B-y_A)|.$

L'aire du triangle ABC peut aussi se calculer à partir de la formule $S=\dfrac{1}{2} \left| \det\begin{pmatrix}x_A & x_B & x_C \\ y_A & y_B & y_C \\ 1 & 1 & 1\end{pmatrix} \right| = \dfrac{1}{2} \big| x_A y_C - x_A y_B + x_B y_A - x_B y_C + x_C y_B - x_C y_A \big|.$

Cette méthode se généralise en trois dimensions. L'aire du triangle ABC où $A = (x A, y A, z A)$ , $B = (x B, y B, z B)$ et $C = (x C, y C, z C)$ s'exprime comme

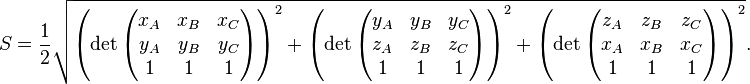
$S=\frac{1}{2} \sqrt{ \left( \det\begin{pmatrix} x_A & x_B & x_C \\ y_A & y_B & y_C \\ 1 & 1 & 1 \end{pmatrix} \right)^2 + \left( \det\begin{pmatrix} y_A & y_B & y_C \\ z_A & z_B & z_C \\ 1 & 1 & 1 \end{pmatrix} \right)^2 + \left( \det\begin{pmatrix} z_A & z_B & z_C \\ x_A & x_B & x_C \\ 1 & 1 & 1 \end{pmatrix} \right)^2 }.$

Contenu soumis à la licence CC-BY-SA. Source : Article Triangle de Wikipédia en français (auteurs)

Évaluer cet élément

(5 Votes)

Publié dans Mathématiques

Dernier de Zesolution.com

Plus dans cette catégorie : Méthode pratique pour calculer un pourcentage »

Retour en haut