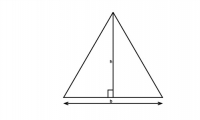
The area of a triangle is the area of the portion of the plane that it encloses. There are several ways to calculate it, depending on the information you want to start from.
Special case of the right triangle
In the case of a right-angled triangle and when we know the width and length of it, just do:
Area = (L * l) / 2
Calculation from a height
If the triangle is right, it is immediate that its area is
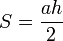
where a is the length of a different side of the hypotenuse and h is the length of the height from that side. If the triangle is not right-angled, the relation remains true, because the triangle breaks up into two right-angled triangles (as in the figure below).
From the lengths of all three sides
For an expression of the area of a triangle whose side lengths are a, b and c and p the half-perimeter [ 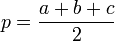 ]
]
, we can use Heron's formula:

From the coordinates of the vertices
The area of the parallelogram defined by two vectors  ,
,  is the norm of their cross product:
is the norm of their cross product:
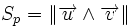
We can calculate the area of a triangle from this formula:
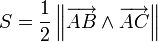 .
.
Given an orthonormal coordinate system, the area of triangle ABC can be calculated from the coordinates of the vertices.
In the plane, if the coordinates of A, B and C are given by A ( x A , y A ) , B ( x B , y B ) and C ( x C , y C ) , then the area S is the half of the absolute value of the determinant
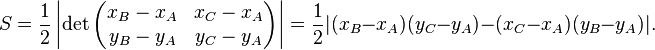
The area of triangle ABC can also be calculated from the formula 
This method is generalized in three dimensions. The area of triangle ABC where A = ( x A , y A , z A ) , B = ( x B , y B , z B ) and C = ( x C , y C , z C ) is expressed as
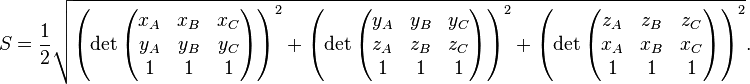
Content subject to CC-BY-SA license . Source: Triangle article from Wikipedia in French ( authors )